SEO de Alta Performance
para Empresas do Rio Grande do Sul
Levamos sua empresa ao topo do Google com SEO técnico, Google Meu Negócio e engenharia de performance. Resultado real, previsível e consistente no RS.
Serviços que Impulsionam Seu Negócio
Atuamos com SEO técnico, Google Meu Negócio, engenharia de performance e criação de sites profissionais. Nossa metodologia combina dados, conteúdo e autoridade digital para gerar crescimento real e previsível para empresas em todo o Rio Grande do Sul.
Por que Escolher a Ti Encontrei?
Entregamos SEO de alta performance, engenharia de performance digital e estratégias baseadas em dados que transformam empresas do Rio Grande do Sul. Nossa metodologia combina técnica, conteúdo, autoridade digital e otimização contínua.
Crescimento Contínuo
Aumento real de impressões, cliques e posições no Google com projeção previsível.
Mais Clientes pelo Google
Estratégias avançadas de SEO Local fortalecem sua presença no Maps e nas buscas regionais.

Engenharia de Performance
Melhorias técnicas profundas que elevam Core Web Vitals, velocidade e estabilidade.

Autoridade Digital Real
Backlinks premium, PR digital e conteúdo estratégico elevam sua autoridade no setor.
Reconhecimento na Mídia
A Ti Encontrei ganhou destaque em portais nacionais e internacionais por sua atuação em SEO técnico, Google Meu Negócio e engenharia de performance. Nossa metodologia levou a marca a ser citada pelo MIT, UOL, Band, Banda B e outros veículos de autoridade — reforçando confiança, expertise e resultados reais.

Quem Somos
Atuamos desde 2017 no mercado de marketing digital, unindo SEO técnico, Google Meu Negócio e engenharia de performance para entregar resultados reais, previsíveis e consistentes.
A nossa missão é elevar empresas ao topo do Google, combinando estratégia, tecnologia e execução profissional — sempre com foco em negócios locais do Rio Grande do Sul.
No dia a dia, a Ti Encontrei desenvolve soluções orientadas por dados, criando sites de alta performance, estratégias de autoridade digital e presença local dominante.
Resultados Reais
Veja alguns exemplos dos resultados obtidos com SEO técnico, Google Meu Negócio e engenharia de performance para empresas do Rio Grande do Sul.

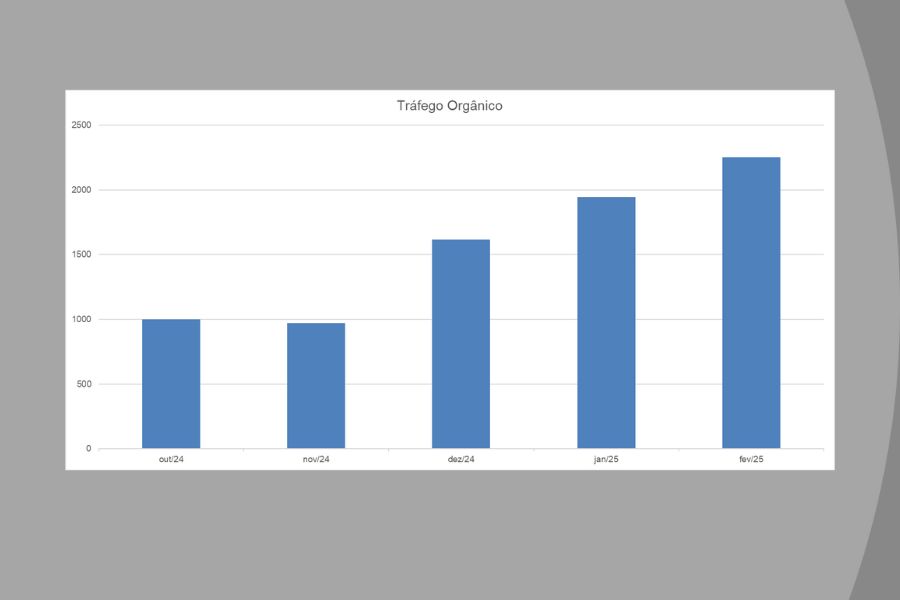
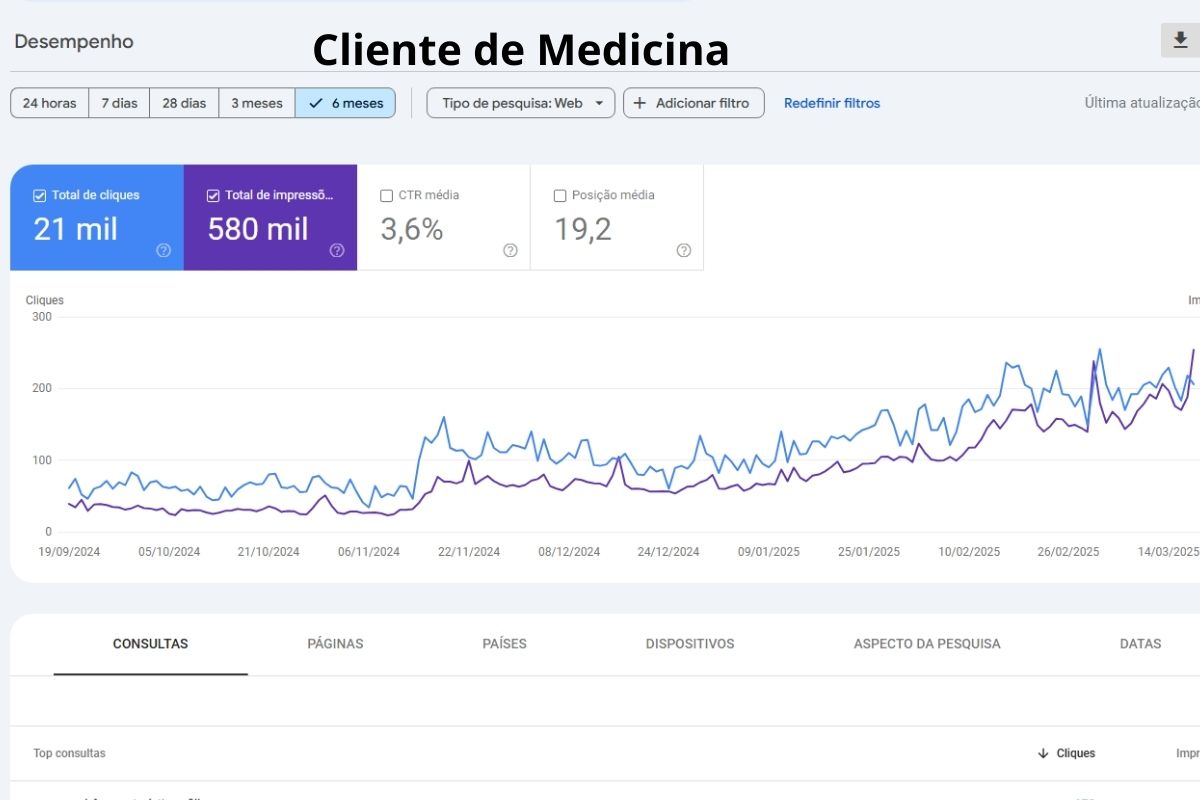
Crescimento de Impressões e Cliques
Gráfico real do Google Search Console mostrando evolução orgânica consistente nos últimos 90 dias.
Mais Clientes pelo Google Maps
Aumento nas ações de rota, mensagens e visitas ao perfil no Google Meu Negócio.

Performance Técnica Otimizada
Melhorias em velocidade, estabilidade visual e índices Core Web Vitals após otimização técnica.
Veja mais conteúdos exclusivos
Artigos selecionados pela Ti Encontrei como destaques estratégicos.
Atuação em Todo o Rio Grande do Sul
A Ti Encontrei fortalece empresas em todas as regiões do RS com SEO técnico, Google Meu Negócio, criação de sites e estratégias de autoridade digital. Nosso foco regional garante resultados consistentes e presencia real nas buscas locais.
Porto Alegre
Caxias do Sul
Bento Gonçalves
Garibaldi
Farroupilha
Gramado
Canela
Santa Cruz do Sul
Pronto para Crescer no Digital?
A Ti Encontrei ajuda empresas do Rio Grande do Sul a se destacar no Google com SEO técnico, Google Meu Negócio, engenharia de performance e autoridade digital. Fale com um especialista e descubra como podemos impulsionar seus resultados.
Falar com um Especialista







